Complexity(복잡도)
Time Complexity (시간복잡도)
: 문제 크기 & 해결 시 걸리는 시간 사이의 관계
시간복잡도 종류
1. 평균 시간복잡도
: 임의의 입력 패턴을 가정했을 때 소요되는 시간의 평균
2. 최악 시간복잡도
: 가장 긴 시간을 소요하게 만드는 입력에 따라 소요되는 시간
* 최선 시간 복잡도 같은건 고려하지않음
Space Complexity (공간복잡도)
: 문제 크기 & 해결 시 필요한 메모리 공간 사이의 관계
Big-O Notation
: 알고리즘 복잡도 표현 시 사용하는 점근 표기법(asymptotic notation) 중 하나
정의는 '어떤 함수의 증가 양상을 다른 함수와의 비교로 표현'한다 인데
복잡도 식에서 상수항과 계수를 제거하면 된다.
예) 2*n^2 → O(n^2)
sort에서 가장 많이 사용하기 때문에, 정렬 공부 시 반드시 기억하기!!
Abstract Data Structures (추상적 자료 구조)
추상적 자료 구조의 종류
Data: 정수, 문자열, 레코드
A set of Operations:
삽입, 삭제, 순회, ..
정렬, 탐색, ..
(*자료구조의 경우 이미지로 설명할 수 있는 부분은 글로 설명하진 않았습니다.)
List
List란?
선형배열로 표현할 수 있다.

Python에서의 사용
원소 추가

원소 찾기



* find: 문자열에서만 사용가능한 index 함수. 값이 없으면 -1 return
원소 삭제

Sort
Python의 sort 방법
| sorted() | 내장함수(built-in function) | 정렬된 새로운 리스트를 얻어낸다 |
| sort() | 리스트의 메서드(method) | 해당 리스트를 정렬해서 변경해준다 |
*공통점: sort할 때 같은 순서라면 절대적인 순서(처음 선언한 순서)에 의존한다!!
Sort 종류
| 삽입 정렬 | 평균 O(n), 최악 O(n^2) |
| 선형 정렬 | O(n) |
| 이진 정렬 | O(logn) |
| merge sort(병합 정렬) | O(nlogn) |
*정렬 알고리즘 중 O(nlogn)보다 낮은 복잡도를 갖는 알고리즘은 없음!
헷갈렸던 문제!
Q: input N개의 수 모든 원소들 사이 대소 관계를 비교해 N*N행렬로 나타내면 복잡도는?
A: O(N^2)이다. for문 두 번 돌려서 확인 가능!
Q: N*N 행렬의 곱을 계산하려면 (matrix multiplication) 알고리즘의 복잡도는?
A: O(N^3)이다! C 행렬의 열과 행을 표시하기 위해 이중 for문을 돌고,
그 for문 안에서 1~N까지 원소들의 곱을 더하는 연산을 위해 for문을 한번 더 돌려야한다!
for i in range(N):
for j in range(N):
for k in range(N):
C[i][j] += A[i][k]*B[k][j]
Search
| Linear Search 선형탐색 | 시간이 리스트 길이에 비례 | O(n) |
| Binary Search 이진탐색 | 정렬되어있는 경우만 가능 | O(log n)(정확히는 log n/log2지만 생략함) |
* 선형탐색은 결국 index 함수와 같다. 즉, 최악의 경우 모든 원소를 다 비교
* 이진탐색은 divide & conquer!! 한번 비교가 일어날 때마다 리스트 반씩 줄임
Binary Search 구현
: 매우매우 중요하니깐 꼭 기억해두자
def solution(L, x):
answer = -1
lower = 0
upper = len(L)-1
while lower <= upper:
middle = (lower+upper)//2
if L[middle] == x:
return middle
elif x < L[middle]:
upper = middle-1
elif L[middle] < x:
lower = middle+1
return answer*middle = (lower+upper)//2 에서 몫을 구하는 것에 주목
Recursive
Recursive(재귀 알고리즘)
: 인간의 생각을 잘 표현한 알고리즘이라고 한다.
'이렇게 하면 되는데 왜 구현이 안되지??'라는 생각이 들때 재귀를 쓰면 아주 유용하다.
근데 공간에서 손해볼 수 있고
Trivial case(종결 조건)을 잘 고려하지 않으면 아주 끔찍한 일이 일어난다.
재귀 깊이 제한을 푸는 마법의 코드!!!
import sys
sys.setrecursionlimit(<type: int, number of limit>)* setrecurs... 안에 원하는 재귀 깊이를 int형으로 넣어주면 된다
대표 예제) 피보나치 수열

재귀의 시간복잡도는?
: 재귀함수에서 시간 복잡도 T(n)을 점화식 T(n) = T(n-1) + c으로 나타낼 수 있다.
이 점화식을 여러 방법으로 해석해서 시간 복잡도를 구할 수 있다.
https://m.blog.naver.com/wns7756/221568348621
재귀함수의 시간복잡도 구하기
재귀적 알고리즘은 시간복잡도를 점화식의 형태로 나타내는 것이 가능하다. 예를들어 다음과 같은 팩토리얼...
blog.naver.com
https://justicehui.github.io/easy-algorithm/2018/03/11/TimeComplexity4/
[시간복잡도] 재귀 알고리즘의 시간복잡도
서론 반복문으로 이루어진 알고리즘은 시간 복잡도를 구하기가 비교적 쉽습니다. 그러면, 재귀 호출로 이루어진 알고리즘의 시간 복잡도는 어떻게 구할까요? 이것이 이 글의 주제입니다.
justicehui.github.io
Linked Lists
연결리스트란?
: 다음의 노드로 이루어진 리스트이다

class Node:
def __init__(self, item):
self.data = item
self.next = None
class LinkedList:
def __init__(self):
self.nodeCount = 0
self.head = None
self.tail = None*이대로 구현할 경우 0번째 노드는 존재하지 않는다
*nodeCount == 0 인 상태는? head = tail = None인 빈 연결리스트 상태
*nodeCount == 1 인 상태는? head = tail = 존재하는 node 1개 인 상태
*nodeCount == 2 인 상태는? head - tail로 이루어진 연결리스트!
연산 정의
1. k번째 원소 참조 하기
: head를 제외하고 k번째 원소일때까지 반복문을 통해 l = l.next
2. 순회하기
: None(=tail이 가르키는 곳)이 나오기 전까지 data를 출력하기
3. 길이 찾기
: nodeCount를 return하기
4. 원소 삽입하기
: 넣고 싶은 위치 pos와, 넣고싶은 노드 newNode를 넣으면 성공 여부를 True/False로 리턴
prev는? 넣고 싶은 위치 pos 바로 직전의 노드!

True일 때 → 위치 pos가 1<= pos <= nodeCount + 1
False일 때 → True의 범위 밖에 있는 경우
*왜 nodeCount + 1도 포함할까? = append한다고 생각하기!
*Corner Case
(1) 맨 앞(pos = 1)일 때: head 조정 필요

(2) 맨 뒤(pos = nodeCount + 1): Tail 조정 필요: tail에서 바로 조정하기
*tail의 경우 prev를 따로 찾지 않아도 prev = tail로 두고 풀면 시간을 줄일 수 있다!

* 원소 삽입의 복잡도는? 맨 앞과 끝에 삽입할 땐 O(1), 그 외 O(n)
4. 원소삭제
: 삭제할 위치 pos가 주어질 때 해당 위치 노드 삭제 후 데이터를 리턴
* 1<= pos <= nodeCount
* 노드 삭제 후 반드시 nodeCount -= 1 해줄것!

*Corner Case
(1) 삭제하려는 node가 맨 앞(pos = 1)일 때: head 조정 필요

(2) 삭제하려는 node가 맨 뒤(pos = nodeCount): tail의 prev를 알아야하고, 조정 필요

*nodeCount == 1 이라면? 태초의 상태로 돌아옴!
self.head = None
self.tail = None
self.nodeCount = 0
*시간복잡도
맨 앞일 때 O(1), 그 외 O(n)
5. 두 리스트 합치기
: L을 입력
self.tail.next = L.head
if L.tail:
self.tail = L.tail
self.nodeCount += L.nodeCount
def getAt(self, pos):
if pos < 1 or pos > self.nodeCount:
return None
i = 1
curr = self.head
while i < pos:
curr = curr.next
i += 1
return curr
def traverse(self):
if not self:
return []
trav = []
curr = self.head
while curr != None:
trav.append(curr.data)
curr = curr.next
return trav
| 배열 | 연결리스트 | |
| 저장공간 | 연속한 위치 | 임의의 위치 |
| 특정 원소 지칭 | 매우 간편 | 선형탐색과 유사 |
| 원소 추가 시간복잡도 | O(1) | O(n) |
+ 더미 헤드를 가지는 연결 리스트?
class LinkedList:
def __init__(self):
self.nodeCount = 0
self.head = Node(None)
self.tail = None
self.head.next = self.tail* 더미헤드가 nodeCount에 영향이 없기 때문에
원소 찾기, 길이 등은 없을 때와 같은 구현을 할 수 있다.
1. 원소 찾기
: pos< 1 or pos > self.nodeCount 일 때 curr= self.head로 시작해서 while문 돌린다!
2. 원소 삽입, 삭제
: 더미노드 = 노드가 하나 더 있음!
즉, 더미헤드가 없을 때 구현한 함수를 그대로 사용하면
원하는 위치 다음의 노드에서 연산이 이루어진다!
그래서 ...After(pos+1에 대해 연산)하는 함수를 만들고
After를 이용해서 ...At(pos에 대해 연산)하는 함수를 구현하자.
*매우매우 쉽다. At(pos) = After(pos-1)이다
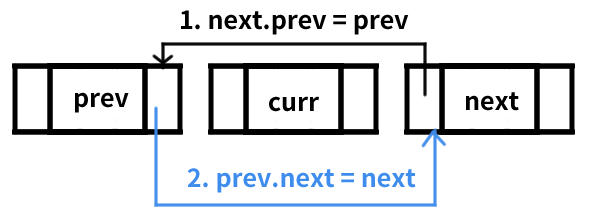
Doubly Linked Lists
양방향 연결리스트란?
: 이전의 노드, 이후의 노드를 접근할 수 있는 노드로 이루어진 리스트이다

class Node:
def __init__(self, item):
self.data = item
self.prev = None
self.next = None
class DoublyLinkedList:
def __init__(self):
self.nodeCount = 0
self.head = Node(None)
self.tail = Node(None)
self.head.prev = None
self.head.next = self.tail
self.tail.prev = self.head
self.tail.next = None
강의에선 insertAfter, insertBefore. insertAt
popAfter, popBefore, popAt을 다 구현하라고 하는데
After, Before하나만 구현해도 At을 구할 수 있다.
그래서 insertAfter, popBefore만 설명한다.
1. insertAfter

2. popBefore
댓글